東工大数学2024(令和6年):東工大首席が解説

はじめまして。
私は東京科学大専門オンライン個別指導:科学大塾で塾長をしている、現役東京科学大(旧 東工大)生です。
主な経歴としては、東工大オープン全学院中一位や、東工大に全学院の首席で合格したことがあります。

今回は、2024年度の東工大数学の過去問を解いていきます。
答案の書き方などを、参考にしていただけると思います。

全体としての感想は、発想を要求する問題が少なく、その点については易化したと言えますが、あいかわらず求められる処理の量が膨大で、試験会場でしっかり完答しきるのは、なかなか難しいセットだったと思います。

※問題については、下記リンクから引用しています。
https://admissions.titech.ac.jp/admissions/admission/admission/first

第一問

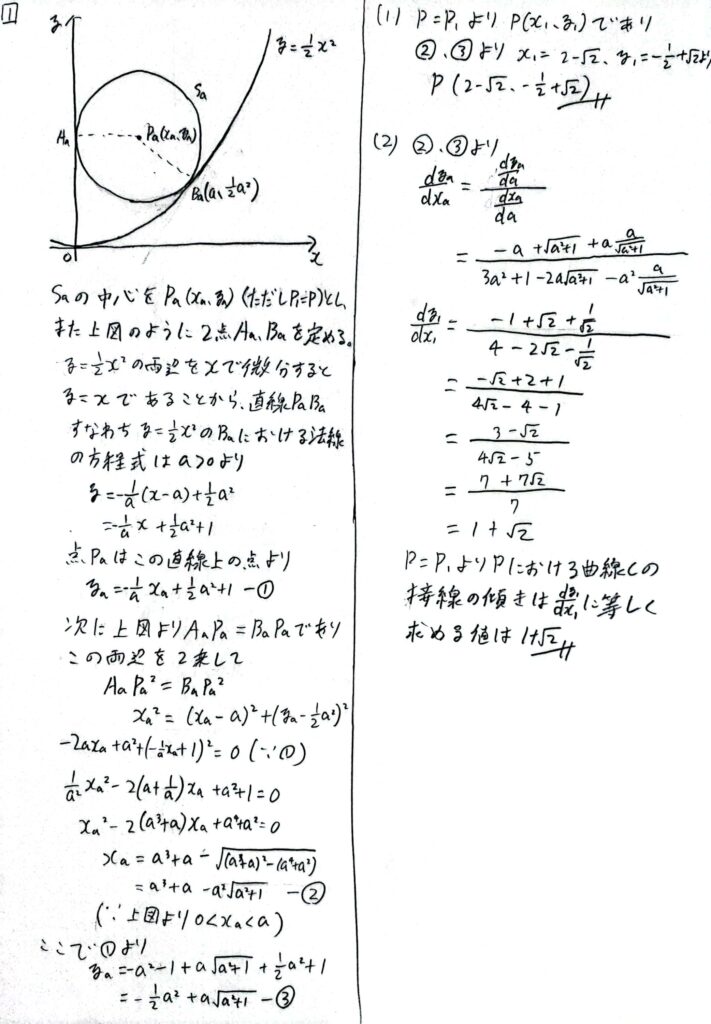
この問題は、発想としては平易なもので、計算量も東工大の中では標準か少ないくらいのものなので、高得点を狙いたい問題だと思います。
ポイントとしては、（１）で点Pの座標という、a=1の場合だけ考えればよい値を求めますが、（２）を見越して、一般のaについて計算する必要があることです。
解き始める前に、大問全体の流れを把握することの大切さが、顕著に表れた一問でしょう。

第二問

第二問がおそらく、多くの受験生にとって、2024年の問題の中で一番、見慣れていなく解きにくかったと思います。
関数方程式という珍しい出題ですが、導関数から元の関数が求まることに気がついてしまえば、残りはよくある問題です。
ただし、答案にも赤字で書きましたが、tan3/8πの値を多くの人は知らないと思うので、最後の積分を解ききれないのはしかたないと思います。（自分ができなかった言い訳ですが…）

第三問

計算量の多い問題でしたが、それだけです。
もし、私の答案のような計算量を抑えた方針が思いつかなくても、愚直な解法で十分解ききれると思います。

第四問

難関大で頻出の確率漸化式の問題です。
（１）（２）は、典型題なので、確実に得点できるようにしたいです。
（３）も計算量こそ多くなってしまいますが、私の答案のように場合分けして解くことで、（１）（２）と同じ考え方を使って解ききることができます。
解いた後に調べてみたところ、（３）はもっと計算量の少ない方法もあるようですが、東工大数学は試験時間が長いこともあり、私のような愚直な解法も全然ありだと思います。
個人的には、試験でやったことのない操作をしたくないので、今回のような愚直な解法を好んで使っています。

第五問

この問題は、実数解をもつときと虚数解をもつときで場合分けできるかで、かなり点数が変わってくると思います。
場合分けさえできてしまえば、a,bが整数であるという条件がかなり強いので、必要条件で解を絞っていき、最後に十分性の確認をすれば、問題なく解ききれるでしょう。（それが難しいんですけど）
似たような問題が、かなり昔の東大で出されていた気がするので、それを知っていた人は簡単だったかもしれません。

投稿者プロフィール

kagakudai-juku

最新の投稿

• 過去問解説2026年1月21日共通テスト2026物理 全問解説｜難化？東工大首席の塾講師が解説
• 勉強論2026年1月19日大学受験は独学で行ける？東工大首席の塾講師が解説！
• その他2026年1月15日2026年度版：共通テスト本番で慌てないための直前確認ポイント
• 東京科学大（旧 東工大）対策2025年6月4日東京科学大学(東工大)の難易度が急上昇!?：令和７年度の合格最低点の変化